动量和动量定理

人教版 高中物理选修3-5

第16章第2节    动量和动量定理

【知识与技能】

1．理解动量定理的确切含义和表达式，知道动量定理适用于变力。

2．会用动量定理解释有关物理现象，并能掌握一维情况下的计算问题。

【过程与方法】

运用牛顿运动定律和运动学公式推导出动量定理表达式。

【情感态度与价值观】

通过运用所学知识推导新的规律，培养学生学习的兴趣。激发学生探索新知识的欲望。

【教学重难点】

★教学重点：理解动量定理的确切含义和表达式

★教学难点：会用动量定理解释有关物理现象，并能掌握一维情况下的计算问题

【教学过程】

★重难点一、对动量的理解★

★对动量的理解

1．动量是状态量

求动量时要明确是哪一物体在哪一状态(时刻)的动量，p＝mv中的速度v是瞬时速度。

2．动量的矢量性

动量的方向与物体的瞬时速度的方向相同，有关动量的运算，如果物体在一条直线上运动，则选定一个正方向后，动量的矢量运算就可以转化为代数运算了。

3．动量的相对性

指物体的动量与参考系的选择有关，选不同的参考系时，同一物体的动量可能不同，通常在不说明参考系的情况下，物体的动量是指物体相对地面的动量。

4．动量与速度、动能的区别和联系

(1)动量与速度

a．区别：速度描述物体运动的快慢和方向；动量在描述物体运动方面更进一步，更能体现运动物体的作用效果。

b．联系：动量和速度都是描述物体运动状态的物理量，都是矢量，动量的方向与速度方向相同，p＝mv。

(2)动量和动能的比较

 

★动量的变化量．

(1)动量是矢量，它的大小p＝mv，方向与速度的方向相同．因此，速度发生变化时，物体的动量也发生变化．速度的大小或方向发生变化时，速度就发生变化，物体具有的动量的大小或方向也相应发生变化，我们就说物体的动量发生了变化．

设物体的初动量p1＝mv1，末动量p2＝mv2，则物体动量的变化：

Δp＝p2－p1＝mv2－mv1

由于动量是矢量，因此，上式一般意义上是矢量式

动量改变有三种情况

①动量的大小和方向都发生变化，对同一物体而言p＝mv，则物体的速度的大小和方向都发生变化；

②动量的方向改变而大小不变，对同一物体来讲，物体的速度方向发生改变而速度大小没有变化，如匀速圆周运动的情况；

③动量的方向没有发生变化，仅动量的大小发生变化，对同一物体来说，就是速度的方向没有发生变化，仅速度的大小改变．

【特别提醒】

动量是矢量，比较两个物体的动量时，不能仅比较大小，也应比较方向，只有大小相等、方向相同的两个动量才能相等。

【典型例题】质量为0.1 kg的小球从1.25 m高处自由落下，与地面碰撞后反弹回0.8 m高处．取竖直向下为正方向，且g＝10 m/s2.求：

(1)小球与地面碰前瞬间的动量；

(2)球与地面碰撞过程中动量的变化．

【审题指导】

(1)小球自由下落时，加速度为g，由速度位移关系公式求出小球碰地前瞬间的速度，再求出动量．

(2)由速度位移关系求出小球碰地后瞬间的速率．取竖直向下方向为正方向，分别表示出碰地前后小球的动量，小球动量的变化量等于末动量与初动量的差

【答案】 (1)小球与地面碰前瞬间的动量为0.5 kg·m/s

(2)球与地面碰撞过程中动量的变化大小是0.9 kg·m/s，方向竖直向上

【解析】(1)设小球从1.25 m高处自由落下碰地前瞬间的速率

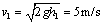
所以小球与地面碰前瞬间的动量

p1＝mv1＝0.1×5 kg·m/s＝0.5 kg·m/s.

（2）取竖直向下方向为正方向，小球碰地后瞬间的速率为

 

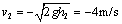
则小球与地面碰撞过程中动量的变化为：

Δp＝mv2－mv1

＝[0.1×(－4)－0.1×5] kg·m/s

＝－0.9 kg·m/s，负号表示方向竖直向上．

★重难点二、对冲量的理解★

★对冲量的理解

1．对冲量的理解

(1)冲量是过程量：冲量描述的是作用在物体上的力对时间的积累效应，与某一过程相对应。

(2)冲量的矢量性：冲量是矢量，在作用时间内力的方向不变时，冲量的方向与力的方向相同，如果力的方向是变化的，则冲量的方向与相应时间内物体动量变化量的方向相同。

(3)冲量的绝对性：冲量仅由力和时间两个因素决定，具有绝对性。

2．冲量的计算

(1)单个力的冲量：利用公式I＝Ft计算。

(2)合力的冲量：

①如果是一维情形，可以化为代数和，如果不在一条直线上，求合冲量遵循平行四边形定则。

②两种方法：可分别求每一个力的冲量，再求各冲量的矢量和；另外，如果各个力的作用时间相同，也可以先求合力，再用公式I_合＝F_合·Δt求解。

③变力的冲量：用动量定理列式求解。

【特别提醒】

(1)冲量是矢量，求冲量的大小时一定要注意是力与其对应的时间的乘积。

(2)判断两个力的冲量是否相同，必须满足冲量的大小和方向都相同，缺一不可。

【典型例题】关于冲量，下列说法正确的是(　　)

A．冲量是物体动量变化的原因

B．作用在静止的物体上的力的冲量一定为零

C．动量越大的物体受到的冲量越大

D．冲量的方向就是物体运动的方向

【答案】A

★重难点三、对动量定理的理解和应用★

1．对动量定理的理解

(1) 动量定理反映了合外力的冲量是动量变化的原因。

(2)动量定理的表达式是矢量式，它说明合外力的冲量跟物体动量变化量不仅大小相等，而且方向相同。

运用动量定理主要是一维的问题，要注意正方向的规定。

(3)动量的变化率和动量的变化量

由动量定理可以得出F＝t(p′－p)，它说明动量的变化率决定于物体所受的合外力。

而由动量定理I＝Δp知动量的变化量决定于合外力的冲量，它不仅与物体的受力有关，还与力的作用时间有关。

2．动量定理的应用

(1)应用动量定理FΔt＝Δp定性解释常见物理现象。

由上式可以看出如果保持Δp一定，则力作用的时间越短，冲力就越大。因此在需要增大作用力时，可尽量减少作用的时间，如打击、碰撞等由于作用时间短、作用力往往较大。反之，作用时间越长，力F就越小，因此在需要减小作用力的时候，可想办法延长力的作用时间，如利用海棉或弹簧的缓冲作用来延长作用时间，达到减小作用力的目的。

(2)应用I＝Δp求变力的冲量。

如果物体受到大小、方向不变的力的作用，既可以应用FΔt求力的冲量，也可以应用物体动量改变Δp的大小和方向来替代力的冲量。

如果物体受到大小、方向改变的力的作用，则不能直接用FΔt求变力的冲量，这时可以求在该力冲量作用下物体动量改变Δp的大小和方向，替代变力的冲量。

3．应用动量定理解题的一般步骤

(1)选定研究对象，明确运动过程。

(2)进行受力分析和运动的初、末状态分析。

(3)选定正方向，根据动量定理列方程求解。

【典型例题】用0．5kg的铁锤把钉子钉进木头里，打击时铁锤的速度v＝4.0m/s，如果打击后铁锤的速度变为0，打击的作用时间是0.01s，(g取10m/s²)那么：

(1)不计铁锤受的重力，铁锤钉钉子的平均作用力是多大？

(2)考虑铁锤受的重力，铁锤钉钉子的平均作用力又是多大？

(3)比较(1)和(2)，讨论是否要计铁锤的重力。

 

【答案】(1)200N，方向竖直向下　(2)205N，方向竖直向下　(3)见解析

【解析】(1)以铁锤为研究对象，不计重力时，只受钉子的作用力，方向竖直向上，设为F₁，取竖直向上为正，由动量定理可得F₁t＝0－mv

所以F₁＝－()0.01(0.5×－4.0)N＝200N，方向竖直向上。

由牛顿第三定律知铁锤钉钉子的作用力为200N，方向竖直向下。

(2)若考虑重力，设此时受钉子的作用力为F₂，对铁锤应用动量定理，取竖直向上为正。

(F₂＋mg)t＝0－mv(矢量式)

F₂＝()0.01(－5×－4.0)N－0.5×(－10)N＝205N，方向竖直向上。

由牛顿第三定律知，此时铁锤钉钉子的作用力为205N，方向竖直向下。

(3)比较F₁与F₂，其相对误差为F1(|F2－F1|)×100%＝2.5%，可见本题中重力的影响可忽略。