课题: 抛物线及其标准方程（第一课时）
学习目标
1、了解抛物线的实际背景，理解抛物线的定义
2、掌握抛物线的标准方程及其推导过程
3、掌握求曲线方程的方法和数形结合的思想
活动体验
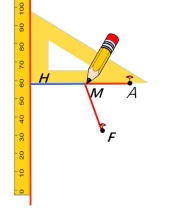按下列步骤作出一条曲线
1.在纸一侧固定直尺
2.将直角三角板的一条直角边紧贴直尺
3.取长等于另一直角边长的绳子，固定绳子一端在直尺外一点F
4.固定绳子另一端在三角板点A上，用笔将绳子拉紧,并使绳子紧贴三角板的直角边
5.上下移动三角板,用笔画出轨迹
作图：
学习过程
(一)形成概念
1.抛物线的定义：平面内与一个定点
和一条定直线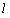
(不经过点)距离____________的点的轨迹叫做抛物线．
2.点叫做抛物线的_________；
3.直线叫做抛物线的_______．
注意点：(1)“一动三定”：一动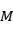点
；一定点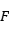
(即焦点)；一定直线
(即准线)；一定值1(即动点到定点的距离与到定直线的距离之比为1).
(2)若点在直线上，点的轨迹是过点且垂直于直线的直线.
想一想? 当直线经过定点，则点的轨迹是什么？
(二)探究方程
类比椭圆、双曲线标准方程的建立过程，你认为如何选择坐标系，求抛物线的方程？
建 系
设点
列等式
代坐标
化简
（三）类比探索
(四)数学应用
